数组

算法思路 - 快慢指针

# 删除有序数组中的重复项 (opens new window)

题目描述

给你一个 升序排列 的数组 nums ，请你原地 (opens new window) 删除重复出现的元素，使每个元素只出现一次，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。将最终结果插入 nums 的前 k 个位置后返回 k 。不要使用额外的空间，你必须在原地 (opens new window) 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

1
2
3

**算法技巧：**快慢指针

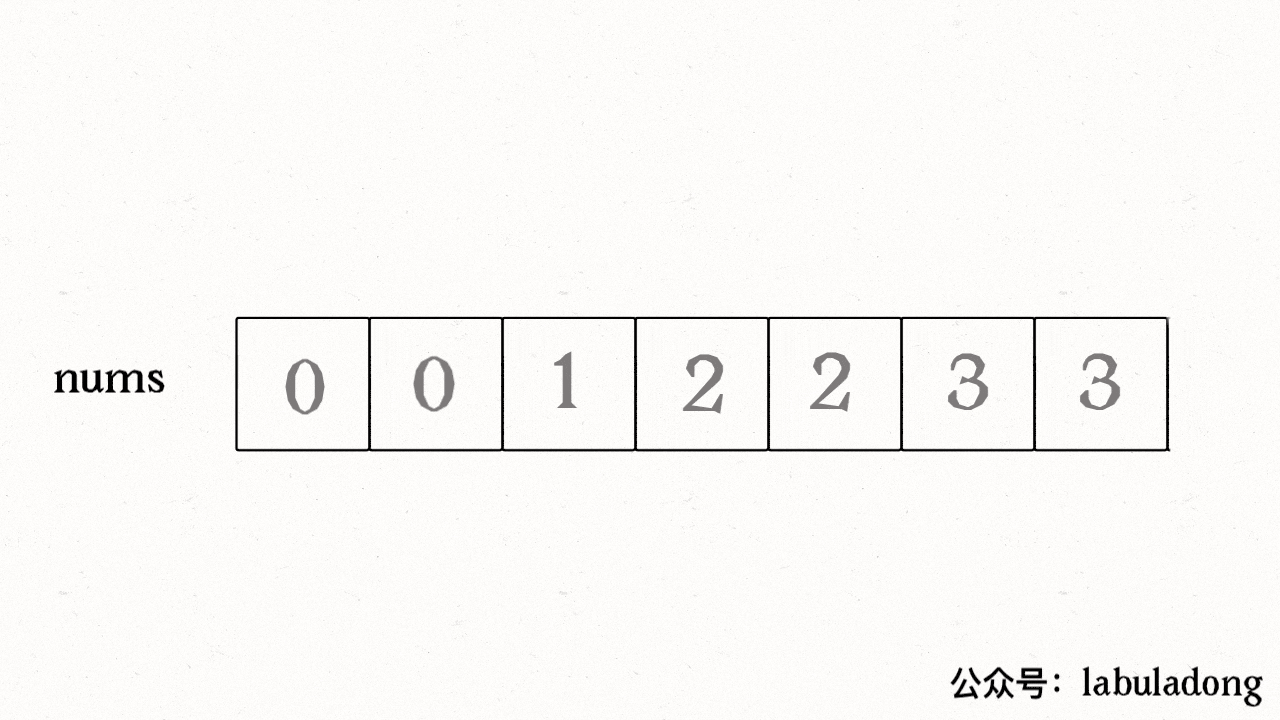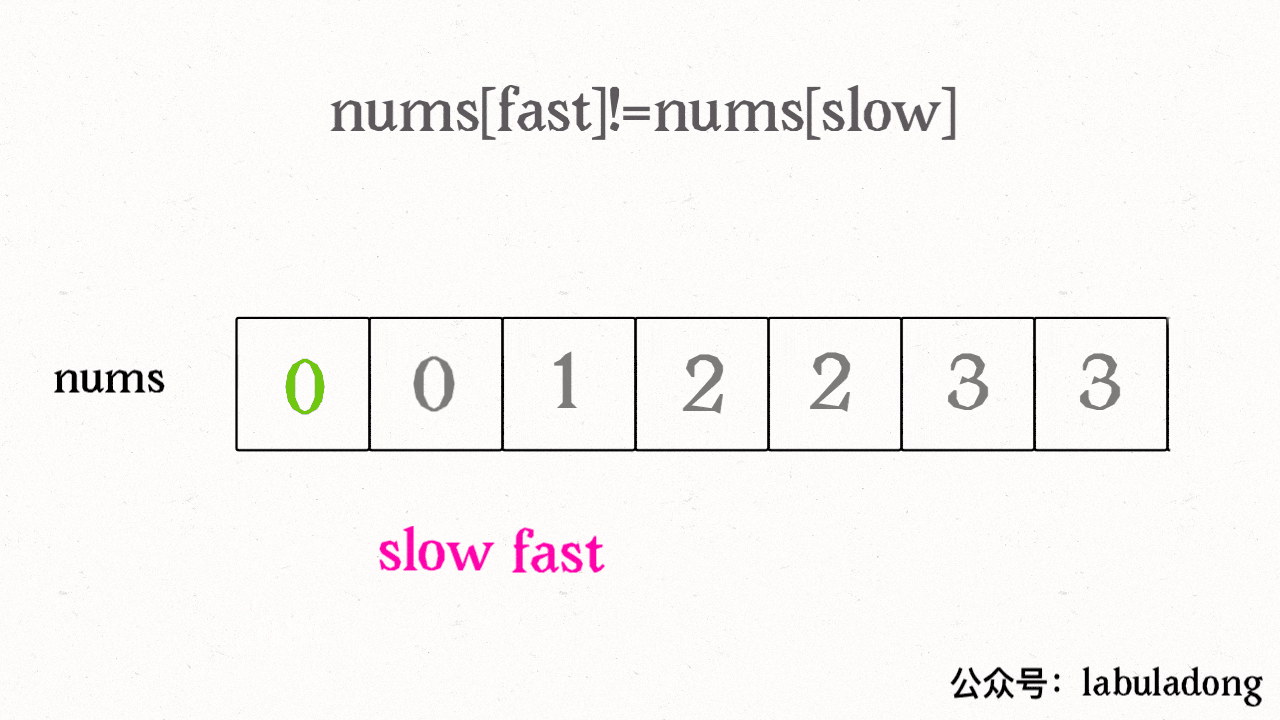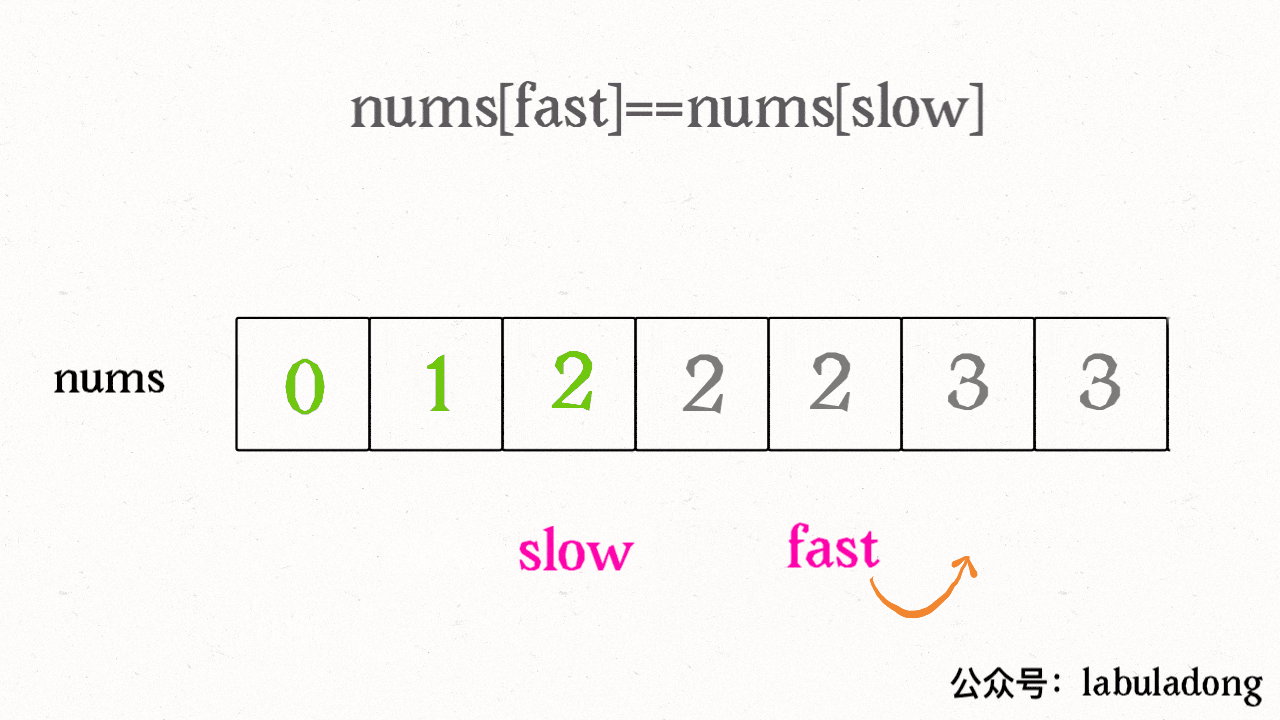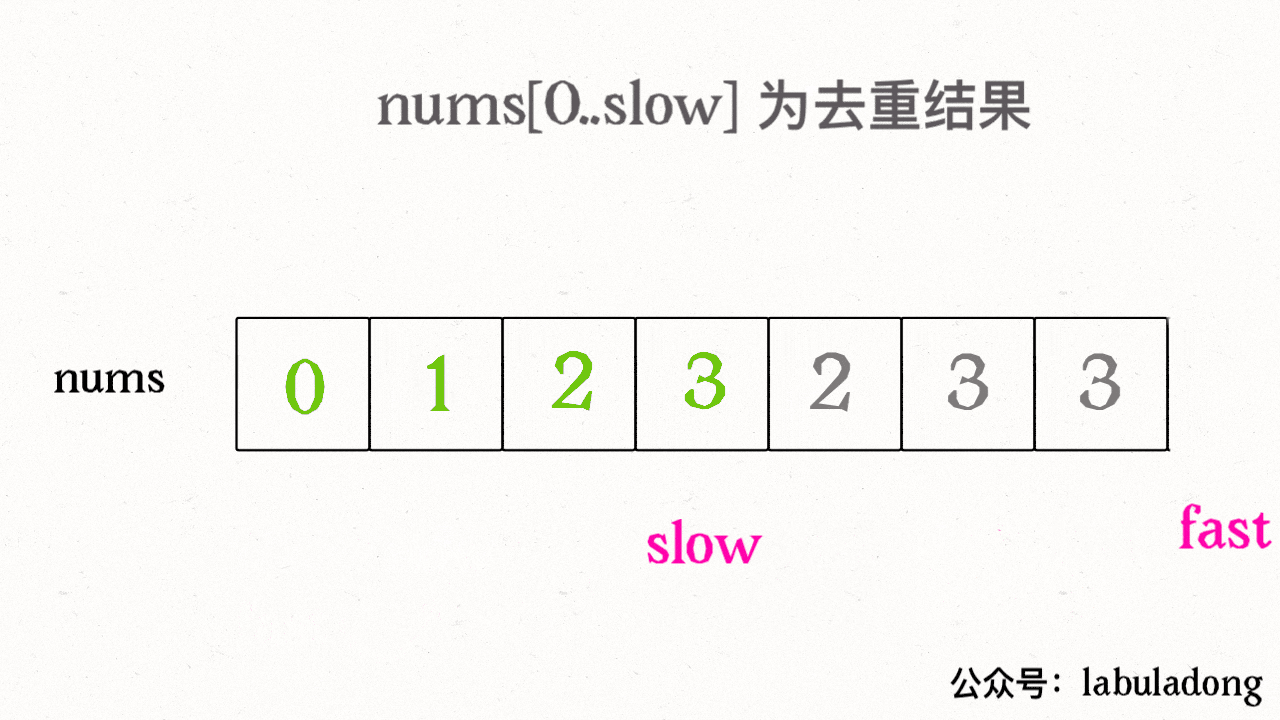
题解

func removeDuplicates(nums []int) int {
    slow := 0
    fast := 0
    lenN := len(nums)
    for fast < lenN {
        if nums[slow] != nums[fast]{
            slow++
            nums[slow] = nums[fast]
        }
        fast++
    }
    return slow+1
}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 移除元素 (opens new window)

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

func removeElement(nums []int, val int) int {
    slow := 0
    fast := 0
    lenN := len(nums)
    for fast < lenN {
        if nums[fast] != val {
            nums[slow] = nums[fast]
            slow++
        }
        fast++
    }
    return slow
}
func removeElement(nums []int, val int) int {
    left := 0
    for _,v := range nums{
        if val != v{
            nums[left] = v
            left ++
        }
    }
    return left
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 移动零 (opens new window)

题目描述

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。请注意，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

1
2

# 快慢指针先移除0，再补0，效率更好

func moveZeroes(nums []int)  {
    lenN := len(nums)
    p := removeElem(nums, 0, lenN)

    //末尾补上0
    for ; p<lenN; p++{
        nums[p] = 0
    }

}

// 移除元素
func removeElem(nums []int, val int, lenN int) int {
    var slow,fast = 0,0

    for fast < lenN {
        if nums[fast] != val {
            nums[slow] = nums[fast]
            slow++
        }
        fast++
    }
    
    return slow    

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# 快慢指针

func moveZeroes(nums []int)  {

    left, right, n := 0,0,len(nums)
    
    for right < n {
        if nums[right] != 0{
            nums[right], nums[left] = nums[left], nums[right]
            left++
        }
        right++
    }

}

1
2
3
4
5
6
7
8
9
10
11
12
13

# 两数之和 II - 输入有序数组 (opens new window)

题目描述

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

1
2
3

题解

func twoSum(numbers []int, target int) []int {
    left := 0
    right := len(numbers) - 1
    for left < right {
        sum := numbers[left] + numbers[right]
        if sum == target {
            return []int{left+1,right+1}
        }else if sum > target {
            right--
        }else {
            left++
        }
    }
    return []int{-1,-1}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

算法思路 - 前缀和数组

# 区域和检索 - 数组不可变 (opens new window)

题目

给定一个整数数组 nums，处理以下类型的多个查询:

计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的和，其中 left <= right

实现 NumArray 类：

NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的总和，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

1
2
3
4
5
6
7
8
9
10
11

题解

type NumArray struct {
    sums []int
}

func Constructor(nums []int) NumArray {
    preSum := make([]int, len(nums))

    for i,v := range nums {
        preSum[i+1] = preSum[i] + v
    }

    return NumArray{preSum}
}

func (this *NumArray) SumRange(left int, right int) int {
    return this.sums[right+1] - this.sums[left]
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 二维区域和检索 - 矩阵不可变 (opens new window)

题目描述

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和。

示例 1：

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
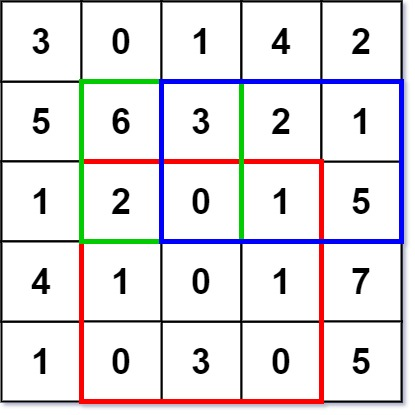
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

1
2
3
4
5
6
7
8
9
10
11

题解

type NumMatrix struct {
    sums [][]int
}


func Constructor(matrix [][]int) NumMatrix {
    // 定义：preSum[i][j] 记录 matrix 中子矩阵 [0, 0, i-1, j-1] 的元素和
    m := len(matrix)
    n := len(matrix[0])
    if n == 0 || m == 0 {
        return NumMatrix{matrix}
    }
    preSum := make([][]int, m + 1)
    preSum[0] = make([]int, n + 1)

 

    for i := 1; i <= m; i++{ // 0,0 到 0,0 不用计算，所以从1开始
        preSum[i] = make([]int, n+1) // todo 注意这一句别漏了
        for j := 1; j <= n; j++{
            // 计算每个矩阵 [0, 0, i, j] 的元素和
            preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i-1][j-1] - preSum[i-1][j-1]
        }
    }

    
    return NumMatrix{preSum}
}


func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
    
    return this.sums[row2+1][col2+1] - this.sums[row1][col2+1]- this.sums[row2+1][col1] + this.sums[row1][col1]
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

算法思路 - 差分数组

# 1109. 航班预订统计 (opens new window)

题目描述

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti （包含 firsti 和 lasti ）的 每个航班 上预订了 seatsi 个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

示例 1：

输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出：[10,55,45,25,25]
解释：
航班编号        1   2   3   4   5
预订记录 1 ：   10  10
预订记录 2 ：       20  20
预订记录 3 ：       25  25  25  25
总座位数：      10  55  45  25  25
因此，answer = [10,55,45,25,25]

1
2
3
4
5
6
7
8
9

题解

func carPooling(trips [][]int, capacity int) bool {
    n := 1001
    // 建立前缀数组
    diff := make([]int, n)
    for _,trip := range trips {
        diff[trip[1]] += trip[0]
        diff[trip[2]] -= trip[0]
    }

	// 计算前缀和
	var preSum int = 0
	for i := 0; i < 1001; i++ {
		preSum += diff[i]
		if preSum > capacity {
			return false
		}
	}
	return true
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

算法思路 - 反转数组

# 旋转图像 (opens new window)

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地 (opens new window)** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

1
2

题解

func rotate(matrix [][]int)  {
    // 先对角线进行反转
    n := len(matrix[0])
    for i:=0; i<n; i++ {
        for j:=0; j<i; j++ {
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        } 
    }

    // 反转数组
    for k,row := range matrix {
        i := 0
        j := len(row) - 1
        for j > i {
            matrix[k][i], matrix[k][j] = matrix[k][j], matrix[k][i]
            i++
            j--
        }
        
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

编辑

#算法 #快慢指针 #前缀和数组 #差分数组

上次更新: 2023/03/13, 15:10:41

链表→